Sorry about the obvious pun in the title. Today's important announcement is of course the long-awaited Planck verdict on the level at which the BICEP2 "discovery" of primordial gravitational waves had been contaminated by foreground dust. That verdict does not look good for BICEP.
(Incidentally, back in July I reported a Planck source as saying this paper would be ready in "two or three weeks". Clearly that was far too optimistic. But interestingly many members of the Planck team themselves were confidently expecting today's paper to appear about 10 days ago, and the rumour is that the current version has been "toned down" a little, perhaps accounting for some of the additional delay. Despite that it's still pretty devastating.)
Let me attempt to summarize the new results. Some important points are made right in the abstract, where we read:
The Planck paper is pretty thorough, and actually quite interesting in its own right. They make use of the fact that Planck observes the sky at many frequencies to study the properties of dust-induced polarization. Whereas BICEP2 was limited to a single frequency channel at 150 GHz, the Planck HFI instrument has 4 different frequencies, of which the most useful is at 353 GHz. Previous Planck results have already shown that dust emission behaves sort of like a (modified) blackbody spectrum at a temperature of 19.6 Kelvin. Since this is a significantly higher temperature than the CMB temperature of 2.73 K, dust emission dominates at higher frequencies, which means that the 353 GHz channel essentially sees only dust and nothing else. Which makes it perfect for the task at hand, since in this particular situation roles are reversed and it is the dust that is the signal and the primordial CMB is noise!
The analysis proceeds in a number of steps. First, they study the power spectra of the two polarization modes (EE and BB) in several different large regions in the sky:
In all these different regions, both power spectra $C_\ell^{EE}$ and $C_\ell^{BB}$ are proportional to $\ell^{\alpha}$, consistent with a value of $\alpha=-2.42\pm0.02$. Fixing $\alpha$ to this value, the amplitude of the power spectra in the different large regions then shows a characteristic dependence on the mean intensity of the dust emission — i.e. regions with more dust overall also show more polarization power — and this purely empirical relationship is characterized by
$$A^{EE,BB}\propto\langle I_{353}\rangle^{1.9},$$though with a bit of uncertainty in the fit. The amplitudes of the polarization power spectra then also show a dependence on frequency from 353 GHz down to 100 GHz which matches previous Planck results (the dependence is something close to a blackbody spectrum at 19.6 K, but with a specific modification).
It then turns out that if the sky is split into very many much smaller regions close to the poles rather than the 6 large ones above, the same results continue to hold on average, though obviously there is some scatter introduced by the fact that dust in different bits of the sky behaves differently. So this allows the Planck team to take the measured dust intensity in any one of these smaller regions and extrapolate down to see what the contribution to the BB power would be if measured at the BICEP2 frequency of 150 GHz. The result looks like this:
This really sucks for BICEP2, who chose their particular patch of the sky precisely because, according to estimates of the 1990s and early 2000s, it was supposed to have very little dust. Planck is now saying that isn't true, and that there is a better region just a little further south. Even that better region isn't perfect, of course, but it may be clean enough to see a primordial GW signal of $r\sim 0.1$ to $0.2$ — if such a signal exists, and if we're lucky and/or figure out cleverer ways of subtracting the dust foreground.
The problem with the BICEP2 region is that Planck's estimate of the dust contribution there looks like this:
Planck avoid explicitly saying that BICEP2 haven't seen anything but dust. This is because they haven't directly measured the dust contribution in that window and at 150 GHz. Rather what's shown in the plot above is based on a number of little steps in the chain of inference:
Incidentally, I have just learned that in two days' time I will be presenting a 30 minute lecture to a group of graduate students about this result. The lecture is not supposed to be very detailed, but I'm also not very much of an expert on this. So if you spot any errors or omissions above, please do let me know through the comments box!
(Incidentally, back in July I reported a Planck source as saying this paper would be ready in "two or three weeks". Clearly that was far too optimistic. But interestingly many members of the Planck team themselves were confidently expecting today's paper to appear about 10 days ago, and the rumour is that the current version has been "toned down" a little, perhaps accounting for some of the additional delay. Despite that it's still pretty devastating.)
Let me attempt to summarize the new results. Some important points are made right in the abstract, where we read:
"... even in the faintest dust-emitting regions there are no "clean" windows in the sky where primordial CMB B-mode polarization measurements could be made without subtraction of foreground emission"and that
"This level [of the dust power in the BICEP2 window, over the multipole range of the primordial recombination bump] is the same magnitude as reported by BICEP2 ..."(my emphasis). Although
"the present uncertainties are large and will be reduced through an ongoing, joint analysis of the Planck and BICEP2 data sets,"from where I am looking unfortunately it now does not look as if there is a realistic chance that what BICEP2 reported was anything more than a very precise measurement of dust.
The Planck paper is pretty thorough, and actually quite interesting in its own right. They make use of the fact that Planck observes the sky at many frequencies to study the properties of dust-induced polarization. Whereas BICEP2 was limited to a single frequency channel at 150 GHz, the Planck HFI instrument has 4 different frequencies, of which the most useful is at 353 GHz. Previous Planck results have already shown that dust emission behaves sort of like a (modified) blackbody spectrum at a temperature of 19.6 Kelvin. Since this is a significantly higher temperature than the CMB temperature of 2.73 K, dust emission dominates at higher frequencies, which means that the 353 GHz channel essentially sees only dust and nothing else. Which makes it perfect for the task at hand, since in this particular situation roles are reversed and it is the dust that is the signal and the primordial CMB is noise!
The analysis proceeds in a number of steps. First, they study the power spectra of the two polarization modes (EE and BB) in several different large regions in the sky:
 |
| The different large sky regions studied are shown as increments of red, orange, yellow, green and two different shades of blue. The darkest blue region is always excluded. Figure from arXiv:1409.5738. |
$$A^{EE,BB}\propto\langle I_{353}\rangle^{1.9},$$though with a bit of uncertainty in the fit. The amplitudes of the polarization power spectra then also show a dependence on frequency from 353 GHz down to 100 GHz which matches previous Planck results (the dependence is something close to a blackbody spectrum at 19.6 K, but with a specific modification).
It then turns out that if the sky is split into very many much smaller regions close to the poles rather than the 6 large ones above, the same results continue to hold on average, though obviously there is some scatter introduced by the fact that dust in different bits of the sky behaves differently. So this allows the Planck team to take the measured dust intensity in any one of these smaller regions and extrapolate down to see what the contribution to the BB power would be if measured at the BICEP2 frequency of 150 GHz. The result looks like this:
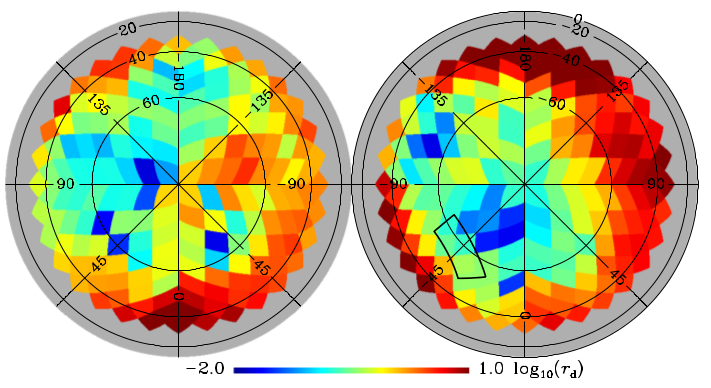 |
| The level of dust contamination across the in measurements of the primordial B-mode signal. Blue is good, red is bad. The BICEP2 window is the black outline on the right. |
The problem with the BICEP2 region is that Planck's estimate of the dust contribution there looks like this:
Planck avoid explicitly saying that BICEP2 haven't seen anything but dust. This is because they haven't directly measured the dust contribution in that window and at 150 GHz. Rather what's shown in the plot above is based on a number of little steps in the chain of inference:
- generally, the BB polarization amplitude is dependent on the average total dust intensity in a region;
- the relationship between these two doesn't vary too much across the sky;
- generally, the frequency dependence of the amplitude shows a certain behaviour;
- and again this doesn't appear to vary too much across the sky
- Planck have measured the average dust intensity in the BICEP2 window, and this gives the value shown in the plot above when extrapolated to 150 GHz;
- and the BICEP2 window doesn't appear to be a special outlier region on the sky that would wildly deviate from these average relationships;
- so, the dust amplitude calculated is probably correct.
Update: See the correction in the comments — the Planck paper actually does better than this. That is to say, they present one analysis that relies on all steps 1-7, but in addition they also measure the BB amplitude directly at 353 GHz and extrapolate that down to 150 GHz relying only on steps 3 and 4. The headline result is the one based on the second method, which actually gets a lower number for the dust amplitude.
So they leave open the small possibility that despite having been unlucky in the original choice of the BICEP2 window, we've somehow ultimately got very lucky indeed and nevertheless measured a true primordial gravitational wave signal.
So they leave open the small possibility that despite having been unlucky in the original choice of the BICEP2 window, we've somehow ultimately got very lucky indeed and nevertheless measured a true primordial gravitational wave signal.
Time will tell if this is true ... but the sensible betting has now got to be that it is not.
Incidentally, I have just learned that in two days' time I will be presenting a 30 minute lecture to a group of graduate students about this result. The lecture is not supposed to be very detailed, but I'm also not very much of an expert on this. So if you spot any errors or omissions above, please do let me know through the comments box!

I completely forgot to mention another interesting thing that Planck reported today. This is that the amplitude of the B-mode polarization is actually lower than would be expected from looking at the level of the E-mode signal. So there's much more dust than previously expected, but that dust appears to be contributing only half as much to the BB signal as we would have thought it would; accounting for these two the end result is still that most of the BICEP signal is likely to be due to dust.
ReplyDeleteBut the question of why there is this discrepancy between the E and B signals is quite interesting in its own right.
It doesn't look like an outlier with respect to the sky, but it does look like it depends on the analysis. Fig. C.3 shows the "detsets" has more power at low ell compared to the other combinations. Is Fig. 9 really an upper bound tracing a systematic correlated among detectors?
ReplyDeleteI don't see the effect you say in Fig. C.3. Looks to me like the points are all consistent with zero within the error bars, especially so in the first bin. How do you conclude that DetSets has systematically more power at low-l?
DeleteThe red points "Detsets-Years" is ~1 sigma high, and the blue points "Halfrings-Detsets" is ~1 sigma low. Fig. 9 uses Detsets. If they had used Years or Halfrings, then the central value would come down by 1 sigma. The statistical error shown in Fig. C.3 a bit of a distraction because the underlying data are the same. You should expect to see quite a bit of correlation, similar to Fig. C.2.
DeleteA more technical point that has me worried is the binning. Why isn't Planck using BICEP2's public band power window functions? I can't find a plot from BICEP2, but they should be similar to BICEP1 http://bicep.rc.fas.harvard.edu/bicep1_3yr/bpwf.png . Is the wide bin just some uniform weight across the ell range assuming all multipoles are independent?
I still don't think that's any evidence that DetSets has systematically more power, since the differences are entirely consistent with noise. If Planck had used the lower values from Years or HalfRings they would of course have got a slightly lower central value of the dust $\mathcal{D}_\ell^{BB}$ in the first bin, but it would be consistent with the current value. They even say in the paper (page 14) that using the average of DetSets, Years and Rings still gives a statistically significant detection of dust in that bin.
DeleteI'm not really qualified to comment on your point about the binning.
Well, of course I will endeavour to remain open-minded :)
ReplyDeleteBut on the point you raise I guess I remain a little unconvinced. For a start the Keck data was supposed to be preliminary, so let's wait to see what the final data says (e.g. the B2xKeck $\ell=50$ band data point is consistent with zero!). Beyond that, you're right that no dust models predict a power spectrum rising with $\ell$ at that scale, but a single data point being a tiny bit low is not really evidence that the BICEP data does rise with $\ell$. Which is I think why Mortonson and Seljak found dust + lensing + no primordial GW provided an acceptable fit to the data ...
Well, M and S only found that because they included Planck temperature data in their fit, which is going to disfavour tensors if you demand a power-law in scalars (which they did). They actually state in the paper that for B-modes alone GW+lensing gives a better fit than dust + lensing.
ReplyDeleteHmm, my memory of what M and S said seems to be wrong. They actually say that, with BICEP2 likelihood alone the r=0 with dust model is still marginally favoured over r=0.2. Of course, one would want to know whether the data favours some sort of combination because there definitely is some dust, but my previous comment was slightly wrong either way.
ReplyDeleteIn replying to your first comment, I was going to say that I find M&S slightly confusing on this point, but I guess you just discovered the same thing too.
ReplyDeleteOn page 4 they say "However, we find that even when considering the BICEP2 likelihood alone, models with $r = 0$ and a polarized dust component fit the BICEP2 data better than models with $r = 0.2$." Later on page 6/7 they say "the BICEP2 data by themselves disfavor a model without gravity waves by $\Delta\chi^2\simeq 11$ relative to the hypothesis of $r = 0.1$ plus dust," but I think that's in the case where the dust amplitude is fixed (to a value slightly lower than the central value Planck quoted today).
More generally, I think the Planck TT power does provide an important prior in a Bayesian comparison of the fit of different alternatives to the BB data!
Planck only gives a 2.3 sigma detection of dust in the BICEP2 patch. This is not very significant so one should be very careful taking it too far "in the other direction".
ReplyDeleteWhere did you get this 2.3 sigma number from? I re-read the paper and couldn't see where it had come from.
DeleteI don't think it can be right anyway. At 353 GHz of course Planck has detected dust in the BICEP2 patch at much higher significance than that. At 150 GHz it may be that the significance of the direct BB power spectrum detection in the BICEP2 patch is lower (though I don't see any mention of 2.3 sigma), but that's the total of dust + GW, and in any case Planck don't really use the direct measurement at 150 GHz except to check consistency of the dust SED.
When extrapolating the very significant 353 GHz dust measurement down to 150 GHz and accounting for the uncertainties in the extrapolation, they get a pretty significant detection of the dust power in the $40<\ell<120$ bin - somewhere between 3.5 and 4.5 sigma, depending slightly on the details of DetSets, Rings etc. So I still don't see where 2.3 sigma comes from.
I'm not sure what the previous anonymous user had in mind, either. He or she may be looking at paper Planck XIX or one of the maps scraped from the slides. The paper Planck XIX only shows "where the systematic uncertainties are small, and where the dust signal dominates total emission." The figures there and others would have the BICEP2 region mostly around the Planck noise floor. The Colley & Gott paper last week agreed, "Thus we conclude that the Planck 353 GHz map in the BICEP2 region is mostly noise sigma_353N = 2.91microK. This includes instrument noise and/or systematic effects." A sudden claim of 4.5 sigma detection in this region is a paradox, at least. The previous anonymous user may instead be noting that the second and third bins are consistent with zero. By combining the 4.5 sigma with two that are consistent with zero, the overall significance could come down.
ReplyDeleteI see. The difference between Paper XIX and this one is that they're using different data. They say they use "a new set of Planck polarization maps for which the systematic effects have been significantly reduced." Section 2.3 says what systematics have been corrected, but I guess we'll have to wait until the 2014 release in one (or two, or three) months' time for full details of how. It does now look like the intensity-to-polarization problem is well under control (from Fig. 2).
DeleteThe Colley and Gott paper used maps scraped from a slide. I can't figure out when that slide dates from, but I think it's unlikely to have contained the new improved data. Plus I think we learned a few months ago that digitizing pdf images adds its own noise. So perhaps that's not the best reference.
Re the level of significance for the dust BB power spectrum in the higher $\ell$ bins at 150 GHz, I'm not really sure how this is relevant to GW, since there's no GW signal to be seen there and lensing will be dominant anyway.
I think it's important to bear in mind what we've really got here, and it isn't much. It's damned statistics, and even if you can dig out a signal that isn't dust, it might not be caused by primordial gravity waves. And waves can be absorbed as well as emitted. I am reminded of a jelly that quivered during it first moment, and then spent 300,000 years in a blender.
ReplyDeleteThe summary you give in the "chain of inference" above is not the punchline of the paper. The Planck team *directly* measures the BB power spectrum in the BICEP2 patch in Section 6 of the paper (Section 6.3: "BB angular power spectrum of dust in the BICEP2 field"). The only extrapolation then required is from 353 GHz (where this power spectrum is measured) to 150 GHz (the BICEP2 frequency). The final result is statistically consistent with the indirect approach mentioned in your "chain of inference", but it is worth emphasizing that a direct measurement is indeed presented -- this is what is shown in Fig. 9 of the paper (not the indirect "chain of inference" result).
ReplyDeleteYes you're right, I got that wrong. Thanks for the correction!
DeleteIf the BICEP2 science team's claim for detection of primordial gravitational waves looks bad, then what is the status for the claims favoring the space roar and/or the photon underproduction crisis? Which experimentalists' claims are most likely to lead to important new theories of physics?
ReplyDeleteMen and women on the exclusive creation inside Jack port Kerouac's Traveling https://imgur.com/a/9bJrX3G https://imgur.com/a/WtH7Aja https://imgur.com/a/Z0cZJ0q https://imgur.com/a/2ZYgD1E http://3n3k193f7w.dip.jp https://imgur.com/a/hnnM9El https://imgur.com/a/pWQFLA8
ReplyDeleteThanks for showing that kind of knowledge on your portal.
ReplyDeleteYou have done all good.
I love to see you again with some new content.
cheapbestfares
Air Flight Tickets
Airline-Ticket-Booking
Airlines Cheap Fares
Best Airline Deals
Black Friday
Book Cheap Flight Tickets
Business Class Flights
Cheap Airline Flights
Flight to California
Must-Do Things Before Starting A Vacation Trip
ReplyDelete10 Things To Do In The Philippines
ReplyDeleteBook a Flight